Einführung in GNU Octave

Hubert Selhofer, mit Änderungen von Marcel Oliver

Date: 2001/11/09

$\includegraphics[height=10cm,angle=270]{sombr.ps}$

1. Grundlagen

Octave ist eine interaktive Scriptsprache, die speziell für vektorisierbare Berechnungen optimiert ist und dabei Standardroutinen der numerischen Mathematik (z.B. EISPACK oder LAPACK) auf einfache Weise zugänglich macht.

Der Syntax von Octave ist dem proprietären Matlab sehr ähnlich, d.h. ein Octave Programm kann meist auch von Matlab ausgeführt werden. Die Rückwärtskompatibilität ist nicht immer gegeben, da Matlab besonders im Grafikbereich um einen erheblich größeren Funktionsumfang verfügt.

1.2 Hilfe!

help listet alle Befehle und internen Variablen auf.
help name gibt Hilfetext zur Variable oder Funktion ,,name`` aus.

Beispiel:

  octave:1> help eig

1.3 Eingabekonventionen

Alle Befehle können sowohl interaktiv, als auch über Skriptdateien eingegeben werden.
Scripts sind Textdateien mit dem Suffix .m. Sie werden durch Aufruf des Dateinamens ohne Suffix eingelesen, und verhalten sich so, als ob ihr Inhalt Zeile für Zeile am Prompt eingegeben würde.
; trennt mehrere Befehle in einer Zeile, und unterdrückt die Zusgabe von Werten.
, trennt Befehle, gibt aber Werte aus.
... am Zeilenende bedeutet, dass der Ausdruck in der nächsten Zeile weitergeht.
Kommentare werden mit % eingeleitet.
Octave unterscheidet zwischen Groß- und Kleinbuchstaben.

1.4 Variablen und Standardoperationen

varname = expression weist varname den Wert expression zu.
Es gibt die ,,üblichen`` Funktionen +, -, *, /, ^, sin, cos, exp, acos, abs, usw.
Die elementaren logischen Operatoren sind:

< kleiner <= kleiner oder gleich & und

> größer >= größer oder gleich | oder

== gleich <> ungleich ~ nicht

Zur Diagnose von benutzerdefinierten Objekten sind folgende Befehle hilfreich:

whos zeigt alle definierten Variablen und Funktionen (siehe Abschnitt 3.1) an.
clear name löscht name aus dem Speicher; falls ,,name`` nicht angegeben wird, werden alle Variablen und Funktionen gelöscht.
type name gibt die Variable oder Funktion name am Bildschirm aus.

Beispiele:

  octave:1> x12 = 1/8, long_name = 'Ein String'
  x12 = 0.12500
  long_name = Ein String
  octave:2> sqrt(-1)-i
  ans = 0
  octave:3> x = sqrt(2); sin(x)/x
  ans = 0.69846

Und hier ein Script doless, der in der Datei doless.m gespeichert ist:

  eins = 1;
  zwei = 2;
  drei = eins + zwei;

Aufruf des Scripts:

  octave:1> doless
  octave:2> whos
  *** local user variables:
  prot  type               rows   cols  name
  ====  ====               ====   ====  ====
   wd   real scalar           1      1  drei
   wd   real scalar           1      1  eins
   wd   real scalar           1      1  zwei

2. Vektor- und Matrixoperationen

Matrizen und Vektoren sind die wichtigsten Grundbausteine zur Programmierung in Octave.

2.1 Vektoren

Zeilenvektor v = (1,2,3):
v = [ 1 2 3 ]
Spaltenvektor: v = (1,2,3)^T:
v = [ 1; 2; 3 ]
Automatische Erzeugung von Vektoren mit konstantem Inkrement:
Anfang[:Inkrement]:Ende

Beispiele:

  octave:1> x = 3:6
  x =
    3  4  5  6
  octave:2> y = 0:.15:.7
  y =
  0.00000  0.15000  0.30000  0.45000  0.60000
  octave:3> z = pi:-pi/4:0
  z =
  3.14159  2.35619  1.57080  0.78540  0.00000

2.2 Matrizen

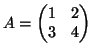Eine Matrix $\displaystyle A = \begin{pmatrix}1 & 2 3 & 4 \end{pmatrix}$ wird erzeugt durch:

  octave:1> A = [ 1 2; 3 4]
  A =
    1  2
    3  4

Matrizen können folgenderweise aus Teilmatrizen zusammengesetzt werden:

  octave:2> b = [5; 6];
  octave:3> M = [A b]
  M =

    1  2  5
    3  4  6

Für einige wichtige $(m \times n)$ -Matrizen existieren eigene Befehle. Falls m gleich n ist, muß nur ein Argument angegeben werden.

eye(m,n) erzeugt eine Matrix mit 1-ern auf der Hauptdiagonale. Im Spezialfall m=n ergibt sich die Einheitsmatrix.
zeros(m,n) erzeugt eine Nullmatrix der Dimension $(m \times n)$ .
ones(m,n) erzeugt eine Matrix der Dimension $(m \times n)$ mit a_ij = 1 $\forall i,j$ .
rand(m,n) erzeugt eine Zufallsmatrix der Dimension $(m \times n)$ mit gleichverteilten Einträgen. Andere Verteilungen siehe help randn.

2.3 Grundlegende Operationen

+, - und * bezeichnen Matrixaddition, -subtraktion und -multiplikation
A' transponiert und konjugiert A.
A.' transponiert A.

Beispiele:

  octave:1> A = [1 2; 3 4]; B = 2*ones(2,2);
  octave:2> A+B, A-B, A*B
  ans =
    3  4
    5  6
  ans =
    -1   0
     1   2
  ans =
     6   6
    14  14

2.4 Elementweise Operationen

Während z.B. * die standard Matrixmultiplikation bezeichnet, gibt es alle Operatoren mit vorangestelltem Punkt für elementweise Verknüpfung: .*, ./, .^, u.s.w.

Beispiele:

  octave:1> A = [1 2; 3 4]; A.^2  % elementweise Potenz
  ans =

     1   4
     9  16

  octave:2> A^2  % Zum Vergleich die matrixweise Potenz
  ans =

     7  10
    15  22

2.5 Indizierung und Slicing

v(k) ist das k-te Element des Zeilen- oder Spaltenvektors v.
A(k,l) ist das Matrixelement a_kl.
v(m:n) ist das ``Slice'' des Vektors v vom m-ten bis zum n-ten Eintrag.
A(k,:) ist die k-te Zeile der Matrix A.
A(:,l) ist die l-te Spalte der Matrix A.

Bestimmung der Größe:

length(v) gibt die Länge des Vektors v zurück.
[Zeilen,Spalten] = size(A) gibt die Anzahl der Zeilen und Spalten von A zurück.

Änderung der Gestalt:

reshape(A,m,n) formt A in eine $(m \times n)$ -Matrix um.
diag(A) liefert die Diagonale a_jj der Matrix A in einem Spaltenvektor.
diag(v) erzeugt eine Matrix mit dem Vektor v auf der Hauptdiagonalen.
diag(v,k) erzeugt eine Matrix mit dem Vektor v in der k-ten Nebendiagonalen.
A(k,:) = zv weist der k-ten Zeile von A den Zeilenvektor zv zu.
A(k,:) = [] löscht die k-te Zeile aus A.
A(:,k) = sv weist der k-ten Spalte von A den Spaltenvektor sv zu.
A(:,k) = [] löscht die k-te Spalte aus A.

Beispiele:

  octave:1> A = [1 2 3; 4 5 6]; v = [7; 8];
  octave:2> A(2,3) = v(2)
  A =

    1  2  3
    4  5  8

  octave:3> A(:,2) = v
  A =

    1  7  3
    4  8  8

  octave:4> A(1,1:2) = v'
  A =

    7  8  3
    4  8  8

2.6 Lösung linearer Gleichungssysteme

A\b löst die Gleichung Ax = b.

Falls A eine $(n \times n)$ -Matrix ist, wird Gaußelimination verwendet, sonst wird via QR-Zerlegung eine Lösung im Sinne der kleinsten Fehlerquadrate berechnet. Ist A schlecht konditioniert oder singulär, wird eine Warnung ausgegeben.

2.7 Inverse, Zerlegungen, Eigenwerte, etc.

B = inv(A) berechnet die Inverse von A.
[L,U,P] = lu(A) berechnet eine LU-Zerlegung LU=PA.
[Q,R] = qr(A) berechnet die QR-Zerlegung QR=A.
R = chol(A) berechnet die Choleskyzerlegung von A.
S = svd(A) berechnet die Singulärwerte von A.
H = hess(A) bringt A in Hessenbergform.
E = eig(A) berechnet alle Eigenwerte von A.
[V,D] = eig(A) berechnet eine Diagonalmatrix D, die die Eigenwerte enthält und eine Matrix V mit den dazugehörigen Eigenvektoren. Es gilt also AV=VD.
norm(X,p) berechnet die p-Norm des Vektors X. Falls X eine Matrix ist, kann p die Werte 1, 2 oder inf haben. Der Default ist p=2.
cond(A) berechnet die Konditionszahl von A in 2-Norm.

Viele dieser Befehle unterstützen weitere Optionen. Diese können Sie mit help funcname erfahren.

2.8 Test auf Nulleinträge

[i,j,v] = find(A) findet die Indizes aller Elemente $\neq 0$ in A Es gilt: $A_{i(l),j(l)} = v_l \neq 0$ .
any(A) ist 1, falls A Elemente $\neq 0$ enthält. Bei Matrizen operiert any auf den Spalten.

3. Kontrollstrukturen

3.1 Funktionen

Traditionell sind Funktionen ebenfalls Textdateien mit Suffix .m. Im Unterschied zu Skripts können Funktionen mit Argumenten aufgerufen werden, und alle innerhalb der Funktion verwendeten Variablen sind lokal (sie beeinflussen die vorher definierten Variablen nicht).

Beispiel:

Eine Funktion f, die in der Datei f.m gespeichert ist.

  function y = f (x)
    y = cos(x/2)+x;
  end

Bemerkung:

In Octave kann man--sinnvollerweise--beliebig viele Funktionen in einer Skriptdatei definieren. Matlab hingegen lässt strikt nur eine Funktion pro .m Datei zu, und der Funktionsname muss mit dem Dateinamen übereinstimmen. Falls Kompatibilität mit Matlab wichtig ist, sollte diese Einschränkung auch auf Octave-Programme angewandt werden.

Beispiel mit zwei Funktionswerten:

Eine Funktion dolittle, die in der Datei dolittle.m gespeichert ist.

  function [out1,out2] = dolittle (x)
    out1 = x^2;
    out2 = out1*x;
  end

Aufruf der Funktion:

  octave:1> [x1,x2]=dolittle(2)
  x1 = 4
  x2 = 8
  octave:2> whos
  *** currently compiled functions:
  prot  type               rows   cols  name
  ====  ====               ====   ====  ====
   wd   user function         -      -  dolittle
  *** local user variables:
  prot  type               rows   cols  name
  ====  ====               ====   ====  ====
   wd   real scalar           1      1  x1
   wd   real scalar           1      1  x2

Offensichtlich waren die beiden Variablen out1, out2 in dolittle lokal. Eine vorher definierte Variable out1 oder out2 wird durch den Aufruf der Funktion nicht beeinflußt.

3.2 Globale Variablen

global name deklariert name als globale Variable.

Beispiel:

Eine Funktion foo in der Datei foo.m:

  function out = foo(arg1,arg2)
  global N % verwende N als globale Variable
  <Berechnung>
  end

Wird N in der Funktion verändert, ändert das auch den ursprünglichen Wert von N im ,,workplace``.

3.3 Schleifen

Die Syntax von for- und while-Schleifen wird an folgenden Beipielen klar:

  for n = 1:10
    [x(n),y(n)]=dolittle(n);
  end

  while t<T
    t = t+h;
  end

For-Schleife rückwärts:

  for n = 10:-1:1
  ...

3.4 Verzweigungen

Bedingte Verzweigungen lassen sich so programmieren:

  if x==0
    error('x ist 0!');
  else
    y = 1/x;
  end

  switch pnorm
    case 1; 
      sum(abs(v))
    case inf; 
      max(abs(v))
    otherwise 
      sqrt(v'*v)
  end

3.5 Funktionen von Funktionen

eval(string) wertet string als Octave-Code aus.
feval(funcname,arg1,) ist äquivalent zum Aufruf von funcname mit Argumenten arg1,.

Beispiel

Berechne mit der Mittelpunktsregel:

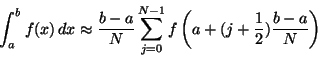
$\begin{displaymath}\int_a^b f(x) dx \approx \frac{b-a}{N} \sum_{j=0}^{N-1} f \left(a + (j+\frac{1}{2}) \frac{b-a}{N}\right) \end{displaymath}$

Die Funktionen gauss.m und mpr.m seien folgendermaßen definiert:

  function y = gauss(x)
    y = exp(-x.^2/2); 
  end

  function S = mpr(fun,a,b,N)
    h = (b-a)/N;
    S = h*sum(feval(fun,[a+h/2:h:b]));
  end

Jetzt kann man die Funktion gauss durch folgenden Aufruf integrieren:

octave:1> mpr('gauss',0,5,500)

3.6 Effizienzüberlegungen

Schleifen und Funktionsaufrufe, insbesondere über den Umweg feval, sind sehr teuer. Deswegen möglichst alle Operationen vektorisieren.

Beispiel:

Wir programmieren die Mittelpunktsregel aus dem vorherigen Abschnitt mit einer for-Schleife (Datei mpr_langsam.m):

  function S = mpr_langsam(fun,a,b,N)
    h = (b-a)/N; S = 0;
    for k = 0:(N-1), 
      S = S + feval(fun,a+h*(k+1/2)); 
    end
    S = h*S;
  end

Man vergleiche die Ausführungszeiten:

  octave:1> t = cputime;
  > Int1=mpr('gauss',0,5,500); t1=cputime-t;
  octave:2> t = cputime;
  > Int2=mpr_langsam('gauss',0,5,500); t2=cputime-t;
  octave:3> Int1-Int2, t2/t1
  ans = 0
  ans = 45.250

3.7 Ein- und Ausgabe

save datei var1 [var2 ] speichert die Variablen var1 usw. in der Datei mit dem Namen datei ab.
load datei liest die Datei datei.
fprintf(string[,var1,]) lehnt sich stark an den Syntax in C an, siehe man fprintf unter Unix.
format [long|short] vergrößert oder verkleinert die Anzahl der ausgegebenen Kommastellen. Der Aufruf ohne Argument stellt das Standardverhalten wieder her.

Beispiel:

  octave:1> for k = .1:.2:.5, 
  > fprintf('1/%g = %10.2e\n',k,1/k); end
  1/0.1 =   1.00e+01
  1/0.3 =   3.33e+00
  1/0.5 =   2.00e+00

4. Grafik

4.1 2D-Grafiken

plot(x,y[,fmt]) zeichnet eine Linie durch die Punkte (x_j,y_j). Mit dem String fmt können Linienart und Farbe gewählt werden (siehe help plot).
semilogx(x,y[,fmt]) Syntax wie plot, die x-Achse wird logarithmisch gezeichnet.
semilogy(x,y[,fmt]) Syntax wie plot, die y-Achse wird logarithmisch gezeichnet.
loglog(x,y[,fmt]) Syntax wie plot, beide Achsen werden logarithmisch gezeichnet.

Soll eine Funktion y=f(x) geplottet werden, geht man praktischerweise folgendermassen vor:

1.

Man erzeugt einen Vektor mit den x-Koordinaten aller zu plottenden Punkte:

  x = x_min:schrittweite:x_max;

(Siehe auch Abschnitt 2.1.)

2.

Man erhält einen Vektor mit den dazugehörigen y-Werten, indem man die funktion f elementweise auf den x-Vektor wirken lässt:

  y = f(x);

Wichtig: Damit f elementweise operiert, müssen die Operatoren .+, .-, .^ usw. anstelle der üblichen +, - und ^ verwendent werden! (Siehe Abschnitt 2.4.)

3.

Jetzt kann man den Plot-Befehl aufrufen:

  plot(x,y); grid; replot

Beispiel:

  octave:1> x = -10:.1:10; 
  octave:2> y = sin(x).*exp(-abs(x));
  octave:3> plot(x,y); grid; replot

$\includegraphics[height=7cm,angle=270]{2d-plot1.ps}$

4.2 3D-Grafiken:

[xx,yy] = meshgrid(x,y) erzeugt aus den Vektoren x und y Gitterdaten.
mesh(x,y,z) zeichnet eine Fläche in 3D.

Beispiel:

  octave:1> x = -2:0.1:2;
  octave:2> [xx,yy] = meshgrid(x,x);
  octave:3> z = sin(xx.^2-yy.^2);
  octave:4> mesh(x,x,z);

$\includegraphics[height=8cm,angle=270]{3d-plot1.ps}$

4.3 Befehle für 2D- und 3D-Grafiken:

title(string) schreibt string als Titelzeile in die Grafik.
xlabel(string) beschriftet die x-Achse mit string.
ylabel(string) beschriftet die y-Achse mit string.
zlabel(string) beschriftet die z-Achse mit string.
axis(v) legt den Ausschnitt fest; v ist ein Vektor der Form v = (xmin, xmax, ymin, ymax[, zmin zmax]).
hold [on|off] legt fest, ob die nächste Grafikausgabe die alte Grafik löschen soll.
clg löscht das Grafikfenster.
replot erzwingt eine erneute Ausgabe der aktuellen Grafik. Dies ist in Octave bei Änderungen einer bestehenden Grafik nötig. (Dieser Befehl existiert nur in Octave und ist auch nur da notwendig.)

5. Übungen

5.1 Lineare Algebra

Erzeugen Sie eine Matrix A und einen Vektor b mit

$\begin{displaymath}A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \quad \text{und} \quad b = \begin{pmatrix} 36 \\ 88 \end{pmatrix}. \end{displaymath}$

Lösen Sie nun das Gleichungssystem Ax = b durch Eingabe von 4Zeichen. Berechnen Sie danach die LU- und QR-Zerlegung sowie die Eigenwerte mit Eigenvektoren von A. Rechnen Sie die Choleskyzerlegung von A^T A aus, und überzeugen Sie sich, dass $\mbox{cond}(A^T A) = \mbox{cond}(A)^2$ ist.

Lösungsvorschlag:

  A = reshape(1:4,2,2).'; b = [36; 88];
  A\b
  [L,U,P] = lu(A)
  [Q,R] = qr(A)
  [V,D] = eig(A)
  A2 = A.'*A;
  R = chol(A2)
  cond(A)^2 - cond(A2)

5.2 Timing

Berechnen Sie ein Matrix-Vektor-Produkt einer $(100 \times 100)$ -Zufallsmatrix mit einem Zufallsvektor, indem Sie einerseits die eingebaute Funktion *, andererseits for-Schleifen verwenden. Vergleichen Sie die Rechenzeiten beider Lösungen.

Lösungsvorschlag:

  A = rand(100); b = rand(100,1);
  t = cputime;  
  v = A*b; t1 = cputime-t;
  w = zeros(100,1);
  t = cputime;
  for n = 1:100,
    for m = 1:100
      w(n) = w(n)+A(n,m)*b(m);
    end
  end
  t2 = cputime-t;

  norm(v-w), t2/t1
  ans = 0
  ans = 577.00

5.3 Stabilitätsfunktionen von BDF-Integratoren

Berechnen Sie alle Nullstellen des Polynoms

$\begin{displaymath}\frac{147}{60}\zeta^6 -6\zeta^5 + \frac{15}{2}\zeta^4 - \fr... ...zeta^3 + \frac{15}{4}\zeta^2 - \frac{6}{5}\zeta + \frac{1}{6} \end{displaymath}$

Hinweis: Verwenden Sie den Befehl compan.

Zeichnen Sie diese Nullstellen in der komplexen Ebene als Punkte ein, und fügen Sie einen Einheitskreis hinzu (Hinweis: hold, real, imag).

Lösungsvorschlag:

  bdf6 = [147/60 -6 15/2 -20/3 15/4 -6/5 1/6];
  R = eig(compan(bdf6));
  plot(R,'+'); hold on
  plot(exp(pi*i*[0:.01:2]));
  if any(find(abs(R)>1))
    fprintf('BDF6 ist instabil\n');
  else 
    fprintf('BDF6 ist stabil\n'); 
  end

$\includegraphics[height=8cm,angle=270]{bdf6.ps}$

5.4 3D-Plot

Zeichnen Sie den Graphen der Funktion

$\begin{displaymath}f(x,y) = \exp(-x^2-y^2) . \end{displaymath}$

Lösungsvorschlag:

  x = -3:0.1:3;
  [xx,yy] = meshgrid(x,x);
  z = exp(-xx.^2-yy.^2);
  mesh(x,x,z);
  title('exp(-x^2-y^2)');
  replot;

5.5 Hilbertmatrix

Berechnen sie für die $(n \times n)$ -Hilbertmatrix H( $n=1,\dots,15$ ) die Lösung des linearen Gleichungssystems Hx = b, b = ones(n,1). Berechnen Sie den Fehler und die Kondition der Matrix und zeichnen Sie die beiden in einem Fenster halblogarithmisch auf. (Hinweis: hilb, invhilb.)

Lösungsvorschlag:

  err = zeros(15,1); co = zeros(15,1);
  for k = 1:15
    H = hilb(k);
    b = ones(k,1);
    err(k) = norm(H\b-invhilb(k)*b);
    co(k) = cond(H);
  end
  semilogy(1:15,err,'r',1:15,co,'x');

5.6 Ausgleichsgerade

Berechnen Sie zu beliebig vorgegebenen Punkten (x_j,y_j), die durch zwei Vektoren x und y gegeben sind, die Ausgleichsgerade (im Sinne der kleinsten Fehlerquadrate). Zeichnen Sie die Punkte und die Gerade.

Lösungsvorschlag:

  function coeff = ausgl(x,y)
    n = length(x);
    A = [x ones(n,1)];
    coeff = A\y;
    plot(x,y,'x');
    hold on
    interv = [min(x) max(x)];
    plot(interv,coeff(1)*interv+coeff(2));
  end

5.7 Trapezregel

Schreiben Sie ein Programm, das beliebige Funktionen f in einer Variablen auf einem Intervall [a,b] numerisch integriert. Verwenden sie die Trapezregel ( h = (b-a)/N):

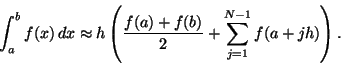
$\begin{displaymath}\int_a^b f(x) dx \approx h\left( \frac{f(a)+f(b)}{2} + \sum_{j=1}^{N-1} f(a+jh) \right). \end{displaymath}$

Verifizieren Sie in einem doppellogarithmischen Bild anhand einer beliebigen Funktion f, dass die Trapezregel Ordnung 2 hat.

Lösungsvorschlag:

  function S = trapez(fun,a,b,N)
    h = (b-a)/N;
    % fy = feval(fun,[a:h:b]); besser:
    fy = feval(fun,linspace(a,b,N+1));
    fy(1) = fy(1)/2;
    fy(N+1) = fy(N+1)/2;
    S = h*sum(fy);
  end

  function y = f(x)
    y = exp(x);
  end  

  for k=1:15; 
    err(k) = abs(exp(1)-1-trapez('f',0,1,2^k));
  end
  loglog(1./2.^[1:15],err);
  hold on;
  loglog(1./2.^[1:15],err,'x');
  title('Trapezregel, f(x) = exp(x)');
  xlabel('Schrittweite');
  ylabel('Fehler');
  replot;

Über dieses Dokument ...

Einführung in GNU Octave

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

The command line arguments were:
latex2html -split 0 -no_navigation -show_section_numbers octave.tex.

The translation was initiated by Marcel Oliver on 2001-12-02

Marcel Oliver
2001-12-02

`<`	kleiner	`<=`	kleiner oder gleich	`&`	und
`>`	größer	`>=`	größer oder gleich	`\|`	oder
`==`	gleich	`<>`	ungleich	`~`	nicht