The Mathematics Curriculum
Main Features
- Students have a choice between two or even three degree
programs until the end of the first year;
- Every student may opt to study abroad for one semester, or do a
semester-long internship in a company or research institute;
- Every student can select a minor subject among a variety of
subject areas.
Study Handbooks
Informal Description
Students may focus on pure or applied mathematics in their second year
of study, or pursue both. It is also possible to select a
minor subject which will become an official part of the degree
transcript. This leads to a large set of degree options tailored
toward individual strengths and interests, e.g.
- Bachelor of Mathematics,
- Bachelor of Mathematics with a minor in Physics,
- Bachelor of Mathematics with a minor in Computer Science,
- Bachelor of Mathematics with a minor in Economics and
Management,
- Bachelor of Mathematics with a minor in Electrical and
Computer Engineering.
Many more major/minor combinations are possible.
The structure of the curriculum is represented in the following
diagram. It represents a typical selection of modules and possible
choices. Jacobs University offers individual advising and provides a
number of options which deviate from the general scheme, including the
fast-tracking of students with exceptional talents, tailored study
options for students with prior university experience, or additional
minor subjects addressing special interests and talents.
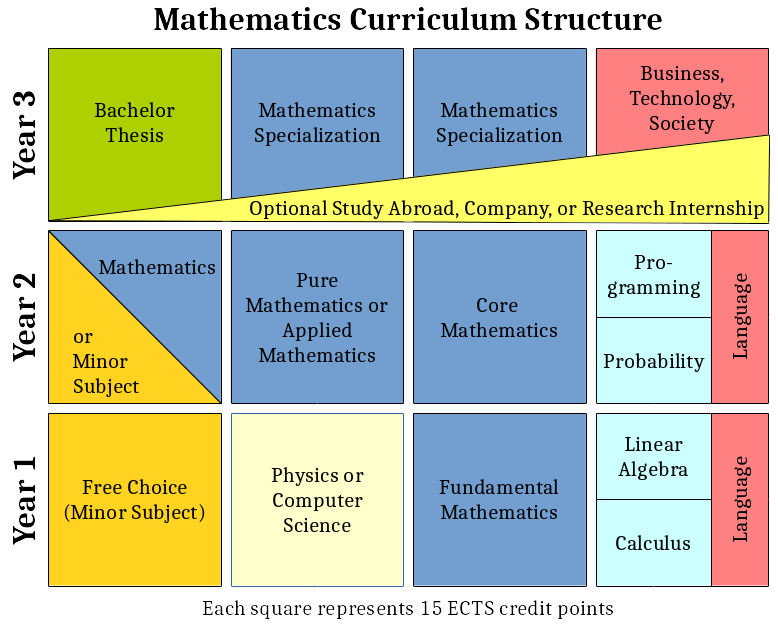
Note: The structure graphics is a simplified version of
the Mathematics curriculum. It is designed to convey the essence of
the program structure, but cannot show every detail or study option.
Exact module and course names are subject to change.
The Study Plan
Year 1
The first year is providing a sound foundation in Mathematics. At the
same time it allows to venture into two other subject areas, at least
one of which should be Physics or Computer Science as
these programs provide additional exposure to mathematics in action.
At least one module is completely free to choose. Thus, it is
possible to study close to Mathematics by selecting Physics
and Computer Science, or venture into areas of independent
interest such as Social
Sciences, Business, Economics, Psychology,
or Chemistry.
As part of the university-wide methods and skills education, students
are strongly encouraged to learn or improve their German if German is
not their mother tongue, or learn a third language if they are already
fluent in German.
Year 2
The second year continues the mathematics core education with one
module common to all mathematics students supplemented by additional
courses from the university-wide methods and skills lineup. In
addition, students select among a pure and an applied mathematics
module, and one module continuing one of the first year choices
outside of mathematics. This leads to the following possibilities:
- A student taking both the pure and the applied mathematics module
will graduate with a Bachelor of Mathematics without a minor.
- A student taking only one of either pure or applied mathematics
will continue another subject into the second year, typically leading
to a Bachelor of Mathematics with a minor.
Year 3
In the fifth semester, students may opt to study abroad, or do a
semester-long internship in a company or in a research lab. Students
who stay on campus will take specialization courses and become
involved in one-one research with a faculty member or junior academic
staff.
The sixth semester offers further specialization options, and all
students work on their Bachelor thesis project. Students with a minor
subject should take at least one specialization course in their chosen
minor.
Over the course of study, Jacobs University requires all students to
take one module worth of credits in the fields of Business,
Technology, and Society. The respective courses will broaden the
horizon beyond the immediate subject area of the chosen major, and
will provide valuable practical skills and concepts that contribute to
success in any one's professional or academic career.
Modules and Courses
Year 1 - Fundamental Mathematics
- General Mathematics: Foundational topics and methods (5 ECTS)
- Analysis II: Continuation of first semester
Calculus/Analysis (5 ECTS)
- Mathematical Software Lab: Mathematica and LaTeX (2.5
ECTS)
- Student Seminar (2.5 ECTS)
Year 2 - Core Mathematics
- Linear Algebra II: Continuation of second semester
Linear Algebra (5 ECTS)
- Introductory Real Analysis: Lebesgue integration and
applications (5 ECTS)
- Numerical Methods (5 ECTS)
Year 2 - Pure Mathematics
- Calculus on Manifolds: Manifolds and differential forms (5 ECTS)
- Introduction to Complex Analysis (5 ECTS)
- Introduction to Algebra (5 ECTS)
Year 2 - Applied Mathematics
- Applied Dynamical Systems + Lab: Nonlinear dynamical
systems with applications (5+2.5 ECTS)
- Stochastic Methods + Lab: stochastic modeling with
applications to finance (5+2.5 ECTS)
Year 3 - Specialization Courses
- Algebra and Geometry
- Manifolds and Topology
- Number Theory
- Discrete Structures and Optimization
- Stochastic Processes and Finance
- Functional Analysis and Elliptic Operators
- Numerical Analysis and Scientific Computing
- Mathematical Modeling with PDEs
- Differential Equations and Dynamical Systems
- Topics in Mathematics (topics of current interest)

