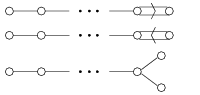
Print version Research Areas in the Mathematical Sciences Algebra and Geometry Alan Huckleberry Complex manifolds Special algebraic varieties Geometry and physics Ivan Penkov Dynkin diagrams of simple Lie algebras (excerpt) Representations of finite- and infinite-dimensional Lie algebras Generalized Harish-Chandra modules: algebraic and geometric constructions Structure and representation theory for locally finite Lie algebras and Lie superalgebras Generalized flag realizations of homogeneous ind-varieties Vector bundles of finite rank on homogeneous ind-varieties Applied Analysis Marcel Oliver Simulation of shallow water flow Partial differential equations: mathematical fluid dynamics geophysical fluid dynamics reaction-diffusion equations Numerical Analysis: structure-preserving algorithms Tobias Preusser PDE-based flow visualization Partial Differential Equations modeling and simulation of biomedical processes mathematical image processing stochastic PDEs for modeling of uncertain parameters scientific visualization with PDEs Numerical Analysis viscosity solutions for geometric PDEs Numerical Methods efficient numerical implementation for image-based-computing multiscale and multigrid approaches Dynamical Systems and Ergodic Theory Keivan Mallahi-Karai The free product of F3 and F6 Infinite groups and their geometric properties Kazhdan's Property (T) Discrete subgroups of Lie groups Dynamics of the Lie group actions and application to number theory Probability Financial Mathematics Igors Gorbovickis 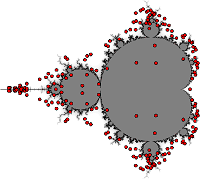Critical points of the multiplier maps equidistribute on the boundary of the Mandelbrot set Dynamical systems Holomorphic dynamics in one and several variables Renormalization in low-dimensional dynamics Thermodynamical formalism in holomorphic dynamics The Mandelbrot set Discrete geometry Kneser-Poulsen conjecture Mathematical Physics Sören Petrat Bose-Einstein condensate Quantum many-body systems Non-linear Schrödinger equation Derivation of effective dynamics Dynamics of Bose-Einstein condensates Hartree-Fock dynamics Spin wave theory Dynamics in the Heisenberg ferromagnet Relativistic quantum mechanics Wave functions on space-time configurations (multi-time wave functions) Peter Schupp Pyrochlor lattice Mathematical Physics Theoretical Particle Physics Non-commutative Geometry Quantum Gravity Quantum Spin Systems Mathematics and its Applications Marc-Thorsten Hütt, Professor of Computational Systems Biology Teaching: Nonlinear Dynamics, Computational Systems Biology Research: Biological networks, genome signatures, analysis of spatiotemporal patterns Ulrich Kleinekathöfer, Professor of Physics Teaching: Computational Physics Research: Computational physics and biophysics, in particular wave function calculations for nonlinear spectroscopy, density matrix theory for electron and exciton transfer, large-scale classical molecular dynamics Agostino Merico, Professor of Ecology Research: Population dynamics, marine ecology, marine geochemistry; paleoclimate; modeling of interactions between climate, ecology, and social and economic systems Joachim Vogt, Professor of Physics Teaching related to ACM: ESS Computational Modeling, ESS Data Analysis Techniques Research: Space physics, computational magnetohydrodynamics, analysis of data from magnetospheric satellite missions Peter Zaspel, Professor of Computer Science Research: Machine learning, data assimilation, uncertainty quantification, approximation in reproducing kernel Hilbert spaces, low-rank approximation, parallel and scalable algorithms     Last updated 2020-08-19, 15:51. © Jacobs University Bremen. All rights reserved. Data Privacy Statement/Datenschutzerklärung